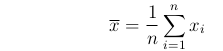Variance
Consider a set of n values: x₁, x₂, ..., x_n , with mean
.

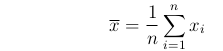The variance of these values, written Var(x) or V(x), is given by:
 

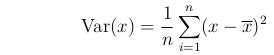
As the name implies, this measures the amount of variation in x. Intuitively, we can think of this as how wide or narrow the probability distribution of values of x is.
 
 
 

Covariance
If we have two variables, say height and weight of people, then we can ask how these covary; that is, to what extent does knowing the value of one give you some information about the other.

The covariance between two variables, written Cov(x,z), is given by:
 

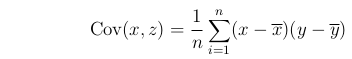
Note that:
 

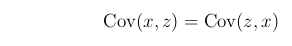
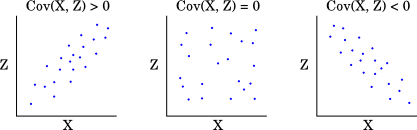
We can think of this as measuring the shape of the distribution of a plot of z vs. x (e.g. a plot of height vs. weight where each point represents one individual person):
 
 
 

Regression
This also measures the dependence of one variable on another.

Consider a plot of one variable against another, like the ones used above to illustrate covariance.

The least squares linear regression (the only kind of regression that we'll use) is the straight line that has the following property:
The sum of the squared vertical distances (yellow in the diagram) of the points from the line is less than for any other straight line.
 
 
 

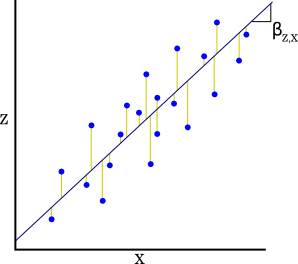
This is called the regression of y on x.

Strictly, the regression is the line, but we will only be concerned with the slope, (z, x). When we are plotting the phenotype of offspring against that of there parents (average of parents for sexual organisms), this slope is the heritability, h².

The regression slope of z on x is the covariance between z and x divided by the variance of x:

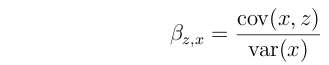
Note that because we are minimizing the sum of squared vertical distances, the regression is not symmetrical, so the regression of z on x is generally not the same as the regression of x on z:
 
 

(The two are equal only when the variances are the same).

All of these values are related to one another like this:
 
 

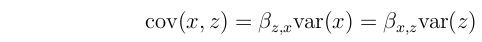
If all of the points lie on a straight line, then the regression of z on x is the same as the derivative, dz/dx. The regression thus allows us to extend the notion of the derivative to cases in which the data points do not all lie on the curve of a simple function. Jul 8, 2021