Section 2-3: Solving Inequalities Using Multiplication or Division (pages 59-64)
Section 2-3: Solving Inequalities Using Multiplication or Division (pages 59-64)
Understanding Mathematical Terms
Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.
Explorations
In Lesson 1, you learned how to use the multiplication and division properties of equality. You will now see the similarity and the difference when you use the multiplication and division properties of inequality.
The direction of the inequality sign can change for two reasons:
- You have multiplied or divided by a negative number.
- You want to make the final solution more readable.
Example:
12 < –3x
![]()
–4 > x
x < –4
Divide by –3 and change the direction of the inequality symbol.
Change the direction of the inequality symbol to read the solution.
Answers to Explorations and Communicate Your Answer
Exploration 1 (page 59)
- 0; 3; 6; 9; 12; 15; no; no; no; yes; yes; yes; right graph; x > 2
- i. x < 2
ii. x ≤ 1
iii. x < 4
iv. x ≤ 2
Dividing each side of an inequality by the same positive number produces an equivalent inequality.
Exploration 2 (page 59)
- 15; 12; 9; 6; 3; 0; –3; yes; yes; yes; no; no; no; no; left graph; x < –2
- i. x > –2
ii. x ≥ –1
iii. x > –4
iv. x ≥ –2
When dividing each side of an inequality by the same negative number, the direction of the inequality must be reversed to produce an equivalent inequality.
Communicate Your Answer (page 59)
- Divide each side of the inequality by the same number. If the number is positive, this produces an equivalent inequality. If the number is negative, the inequality must be reversed to be equivalent.
- a. x < –3
b. x ≥ 3
c. x < –2
d. x ≥ 0
Section 2-3 Lesson (pages 60-62)
Study and work through Examples 1 through 3. Remember, what you do to one side you must do the other side and when you change the direction of the sign. Practice with the Monitoring Progress problems as you go, and then check your answers below.
Answers to Monitoring Progress (pages 60-62)
- n ≥ –7
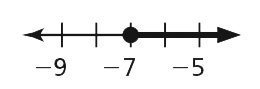
- w ≤ –32
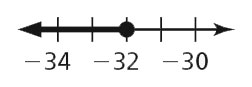
- b ≥ 9
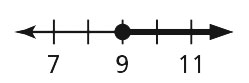
- q < –12
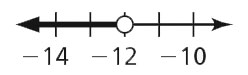
- p > –28
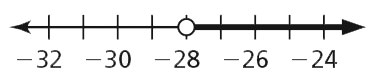
- x ≥ 25
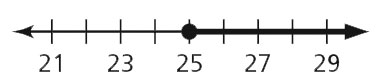
- z ≥ –10
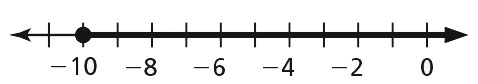
- m < –7
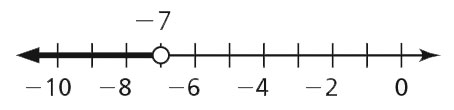
- r ≤ 11

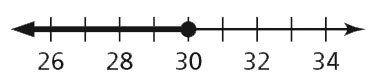
- y ≤ 30
- 0.25c ≤ 3.65, c ≤ 14.6
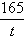 ≤ 55, t ≥ 3
≤ 55, t ≥ 3
Texas Tech K-12
-
Address
Texas Tech Plaza | 1901 University Ave, Lubbock, TX 79401 -
Phone
(800) 692-6877 -
Email
ttuk12@ttu.edu

