Section 2-5: Solving Compound Inequalities (pages 73-78)
Section 2-5: Solving Compound Inequalities (pages 73-78)
Understanding Mathematical Terms
Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.
Explorations
In this section, you will solve problems by making a diagram. You will also solve compound inequalities and graph their solution sets. Any time you draw a picture, you can get a better idea of how to solve a problem. Graphing is a way of drawing this picture to help you find the problem. Each problem in this section will have three graphing lines, as shown in the following example.
Example: Graph the solution set of x > –3 and x ≤ 5.
Draw three number lines. The first will graph the first equation and the second will graph the second equation.
![]()
![]()
Solution: The third graph shows the overlap from the first two graphs.
Notice that this compound inequality, by using the word and, has a solution set that overlaps on the number line.
![]()
Solution set: {x | –3 < x ≤ 5}
A compound inequality that uses the word or will also use three number lines, but the third number line will look very different from the one above. It will not have an overlap. The word or indicates the union of these two different sets of numbers as solutions to the compound inequality.
Read and work through the Explorations and Communicate Your Answer on page 73. Then, check your answers below.
Answers to Explorations and Communicate Your Answer
Exploration 1 (page 73)
- x ≥ –6 and x < 3
- x > –5 and x ≤ 4
- x ≥ –4 and x ≤ 5
- x > –3 and x < 6
- and; Both inequalities need to be true for values that are in the interval.
Exploration 2 (page 73)
- x ≤ –6 or x > 3
- x < –5 or x ≥ 4
- x ≤ –4 or x ≥ 5
- x < –3 or x > 6
- or; Either inequality needs to be true for values that are in the interval.
Communicate Your Answer (page 73)
- Write 2 inequalities joined by "and" or "or."
Section 2-5 Lesson (pages 74-76)
It’s important to remember the difference between graphs of and problems and graphs of or problems. Remember:
- and means intersection (or overlap), so the third graph will show the place where points from the graphs of equation one and two intersect.
- or means union, so the third graph will unify the different solution sets, with all points from the first equation’s graph shaded separately from all of the points from the second equation’s graph.
Study and work through Examples 1 through 4. Practice with the Monitoring Progress problems as you go, and then check your answers below.
Answers to Monitoring Progress (pages 74-76)
- 0 < d < 10
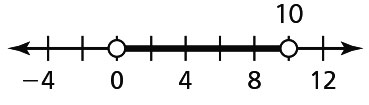
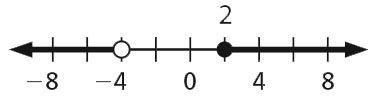
- a < –6 or a ≥ –3
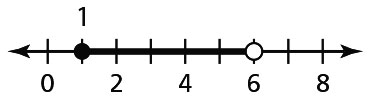
- 1 ≤ m < 6
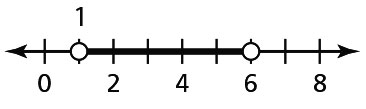
- 1 < k < 6
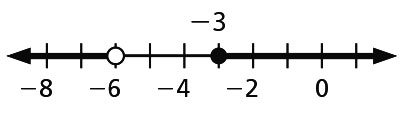
- c ≤ –2 or c > 7
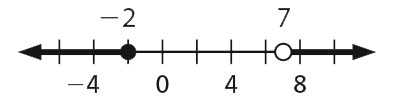
- p < –4 or p ≥ 2
- –40 ≤
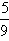 (F – 32) ≤ 15, –40 ≤ F ≤ 59
(F – 32) ≤ 15, –40 ≤ F ≤ 59
Remember also, if you get stuck, you can go to Big Ideas Math. You will have access to the odd numbered problems and the on-line tutor.
Texas Tech K-12
-
Address
Texas Tech Plaza | 1901 University Ave, Lubbock, TX 79401 -
Phone
(800) 692-6877 -
Email
ttuk12@ttu.edu

