Understanding Mathematical Terms

Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.

Explorations

As you read and work through Explorations 1 and 2 and Communicate Your Answer on page 89, be sure to question yourself so that you understand what the statements are saying. You must know the difference between a relation and a function. After finishing Explorations 1 and 2 and Communicate Your Answer, check your answers below. Examples of functions:

Words: adding 2 to input get output

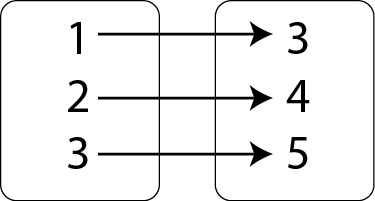
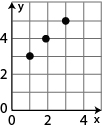
Listing Ordered Pairs: (1, 3), (2, 4), (3, 5)

Equation: y = x + 2

Input-Output Table:

Mapping Diagram:

Graph:

Answers to Explorations and Communicate Your Answer

Exploration 1 (page 89)

1. Each x-coordinate is paired with exactly one y-coordinate.
2. Sample answer: (0, 8), (1, 6), (2, 4), (3, 2), (4, 0);
   

   Input, x	0	1	2	3	4
   Output, y	8	6	4	2	0

Exploration 2 (page 89)

1. function; Each input value is paired with exactly one output value.
2. not a function; The input value of 8 is paired with more than one output value.
3. not a function; The input value of 3 is paired with more than one output value.
4. not a function; The input values of 5 and 7 are each paired with more than one output value.
5. function; Each input value is paired with exactly one output value.
6. not a function; The input value of –1 is paired with more than one output value.
7. function; Each input frequency is paired with exactly one output radio station.
8. not a function; Each input television station is paired with more than one output channel.
9. not a function; The input value of 2 is paired with every possible output value of y.
10. function; Each input value of x is paired with exactly one output value of y.

Communicate Your Answer (page 89)

3. a relation that pairs each input with exactly one output.
   a. Sample answer: (0, 10), (1, 20), (2, 30); y = –5x
   b. Sample answer: (0, 10), (0, 20), (0, 30); x = –5

Section 3-1 Lesson (pages 91-93)

Study and work through Examples 1 through 5. They are very well written and explained. The Vertical Line Test makes it easy to identify a function. You can identify a function by checking all of the ordered pairs (using a mapping diagram) or by checking the graph of an equation using the vertical-line test. If you draw a vertical line through a graph, and that line only touches one point of the graph, then there is only one value of y (range) for every value of x (domain), and the graph illustrates a function.

Be sure to study page 93 on independent and dependent variables. Practice with the Monitoring Progress problems as you go, and then check your answers below.

Answers to Monitoring Progress (pages 91-93)

1. not a function; The input 5 has two outputs, 0 and 10.
2. function; Every input has exactly one output.
3. function; Every input has exactly one output.
4. function; Every input has exactly one output.
5. function; No vertical line can be drawn through more than one point on the graph.
6. not a function; A vertical line can be drawn through more than one point on the graph at several places, such as (3, 0) and (3, 6).
7. domain: –2, –1, 0, 1, 2; range: 0, 2, 4
8. domain: 1 ≤ x ≤ 5; range: 0 ≤ y ≤ 4
9. a. a is the dependent variable and b is the independent variable.
   b. 14, 10, 6, 2
10. a. t is the dependent variable and m is the independent variable.
    b. domain: 0 ≤ m ≤ 15; range: 65 ≤ t ≤ 350