Understanding Mathematical Terms

Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.

Explorations

As you read and work through Explorations 1 and 2 and Communicate Your Answer on page 107, make sure to pay attention to function notation. It can sometimes be confusing. The notation f(x) is read as "the value of f at x" or "f of x." It does not mean "f times x." Think about these instances where parentheses do not mean multiplication:

8 + (−3) = 5

GCF(8, 2) = 4

LCM(8, 12) = 24

P(tossing heads) =  

After finishing Explorations 1 and 2 and Communicate Your Answer, check your answers below.

Answers to Explorations and Communicate Your Answer

Exploration 1 (page 107)

1. B
2. D
3. A
4. C

Exploration 2 (page 107)

1. (–1, 4)
2. (0, 3)
3. (1, 2)
4. (2, 1)

Communicate Your Answer (page 107)

3. Replace "y" with "f(x)" in the equation; They both give the rule for determining the output; Standard notation uses "y" to indicate the output, function notation uses "f(x)" to indicate the output.

Section 3-3 Lesson (pages 108-110)

Study and work through Examples 1 through 5. You will use what you know about evaluating expressions and about solving equations. Practice with the Monitoring Progress problems as you go, and then check your answers below.

Answers to Monitoring Progress (pages 108-110)

1. –13; –5; 1
2. 3; –1; –4
3. a. The temperature is 75℉ at 1 p.m.
   b. The temperature is 70℉ m hours after 9 a.m.
   c. The temperature at 11 a.m. is the same as the temperature at 6 p.m.
   d. The temperature at 3 p.m. is greater than the temperature at 9 a.m.
4. x = 2
5. x = 8
6. 
7. 
8. 
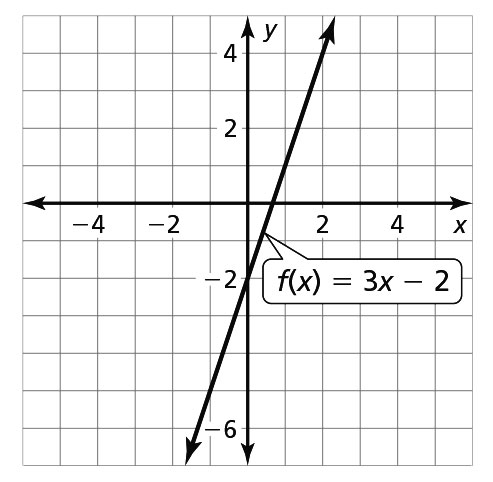
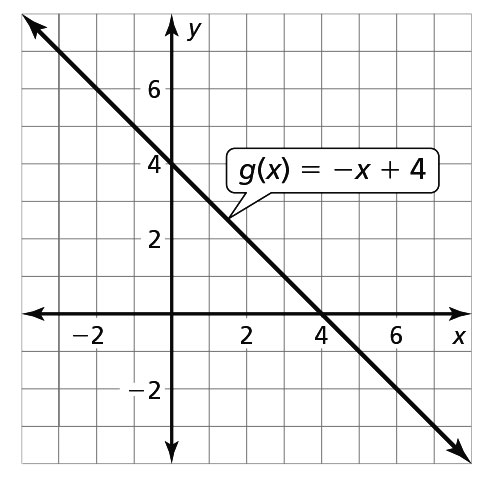
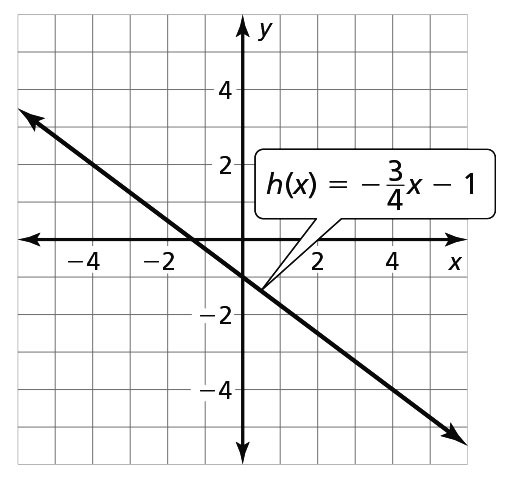
9. the first flight; The graph of the second flight shows that when f(x) = 0, x is slightly more than 3.