Understanding Mathematical Terms

Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.

Explorations

You have graphed proportional and non-proportional relationships and interpreted the unit rate as the slope of the line that models the relationship. You also represented linear proportional situations with tables, graphs, and equations in the form of y = kx. Proportional relationships are referred to as direct variation. The constant of proportionality is called the constant of variation. Read and work through the Explorations 1 and 2 and Communicate Your Answer on page 133. Then, check your answers below.

Answers to Explorations and Communicate Your Answer

Exploration 1 (page 133)

1. yes; The line passes through the origin.
2. no; The line does not pass through the origin.
3. no; The line does not pass through the origin.
4. yes; The line passes through the origin.
5. no; The rate of change is not constant.
6. yes; The rate of change is constant, and the relation can be represented by the equation y = 2x.

Exploration 2 (page 133)

part (a): 10, 10; part (d); 6, 6;

part (f): 2, 2; They are the same; the value of a in the direct variation equation

Communicate Your Answer (page 133)

3. Sample answer: The graph of the data is a line that passes through the origin.
4. Sample answer: gallons of gas and price; y = 3.5x, where x is the number of gallons of gasoline and y is the total cost (in dollars)
   

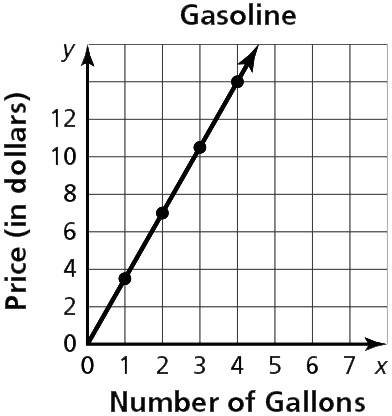
Section 3-6 Lesson (pages 134-136)

Study and work through Examples 1 through 4. Read them carefully. Practice with the Monitoring Progress problems as you go, and then check your answers below.

Answers to Monitoring Progress (pages 134-136)

1. no
2. yes; –2
3. yes; 
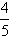
4. yes; The ordered pairs lie on a line that passes through the origin.
5. no; The ordered pairs lie on a line that does not pass through the origin.
6. no; The equation that represents this situation is not of the form y = ax.
7. 750 lb