Section 4-2: Writing Equations in Point-Slope Form (pages 167-172)
Section 4-2: Writing Equations in Point-Slope Form (pages 167-172)
Understanding Mathematical Terms
Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.
Explorations
Read and work through the Explorations 1 and 2 and 3 and Communicate Your Answer on page 167. The point-slope form is first derived by writing the formula for slope between (x, y) and ![]() . To write the equation, you are given the slope and a point, two points, or a context from which the slope and an ordered pair can be deduced. Then, check your answers below.
. To write the equation, you are given the slope and a point, two points, or a context from which the slope and an ordered pair can be deduced. Then, check your answers below.
Answers to Explorations and Communicate Your Answer
Exploration 1 (page 167)
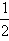 ; y =
; y = 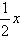 +
+ 
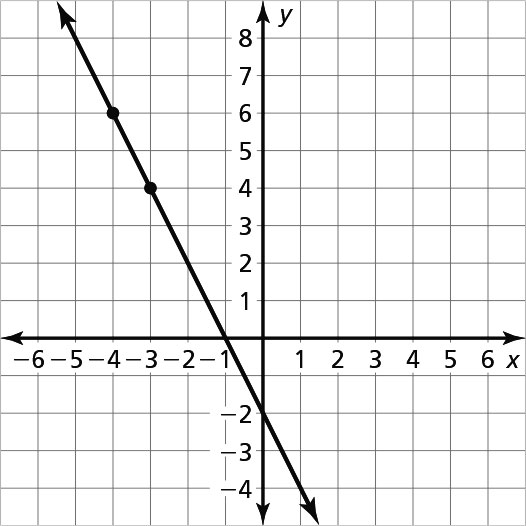
–2; y = –2x – 2
Exploration 2 (page 167)
![]()
; ![]()
Exploration 3 (page 167)
- A = 25t + 75
- Check students' work
Communicate Your Answer (page 167)
- Substitute the slope for m and the coordinates of the point for
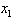 and
and 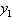 in
in 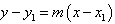 .
. - Sample answer: An equation of the line that passes through the point (2, –9) and has a slope of
 is
is
y + 9 =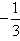 (x – 2).
(x – 2).
Section 4-2 Lesson (pages 168-170)
Read and study Examples 1 through 5. Look carefully at the information you are given in each example. Practice with the Monitoring Progress problems as you go, and then check your answers below.
Answers to Monitoring Progress (pages 169-170)
- –2; Sample answer:
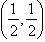
- y + 1 = –2(x – 3)
- y =
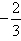 (x – 4)
(x – 4) - y = 3x + 1
- y =
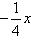 – 2
– 2 - g(x) =
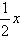 + 2
+ 2 - g(x) = –3x + 5
- yes; The total cost increases at a constant rate; C = 42n + 50
Texas Tech K-12
-
Address
Texas Tech Plaza | 1901 University Ave, Lubbock, TX 79401 -
Phone
(800) 692-6877 -
Email
ttuk12@ttu.edu

