Section 4-7: Arithmetic Sequences (pages 201-208)
Section 4-7: Arithmetic Sequences (pages 201-208)
Understanding Mathematical Terms
Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.
Explorations
Read and work through the Exploration 1 and Communicate Your Answer on page 201. This lesson will make connections between the arithmetic sequences and linear equations. You can use your graphing calculator with this exploration if you want to. Use your STAT Plot feature. Then, check your answers below.
Answers to Explorations and Communicate Your Answer
Exploration 1 (page 201)
- 10, 20, 30, 40, 50
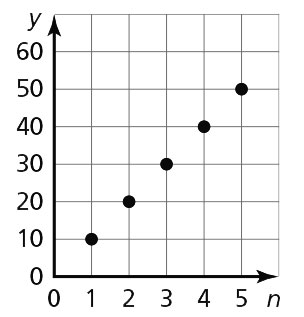
The y-value increases by 10 each time. - 2, 3, 4, 5, 6
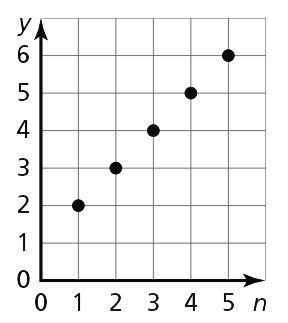
The y-value increases by 1 each time. - 2, 4, 6, 8, 10
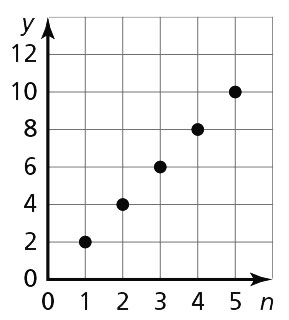
The y-value increases by 2 each time.
Communicate Your Answer (page 201)
- An arithmetic sequence can describe a pattern in which the difference between consecutive terms is the same; Sample answer: The amount of money earned for selling candy bars at $2 each.
- Each molecule added to the group increases the number of atoms by 3; 69 atoms
Section 4-7 Lesson (pages 202-205)
In this lesson, you will write the terms of an arithmetic sequence and extend a given sequence. When the arithmetic sequence is graphed, the result is a line and the slope is the common difference. The last skill in the lesson is writing the arithmetic sequence as an equation and as a function.
Study and read through Examples 1 through 5. Be especially careful with Examples 4 and 5. Practice with the Monitoring Progress problems as you go, and then check your answers below.
Answers to Monitoring Progress (pages 202-205)
-
36, 48, 60
-
1.8, 2.2, 2.6
-
3, 2
 , 2
, 2 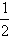
-
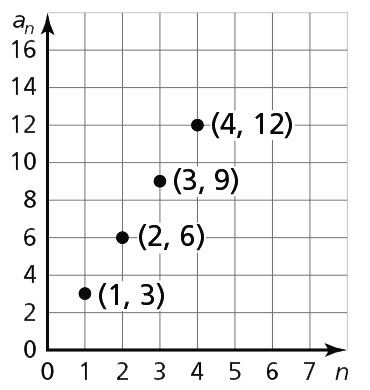
The points lie on a line. -
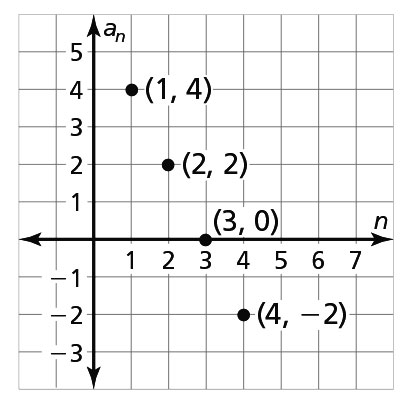
The points lie on a line. -
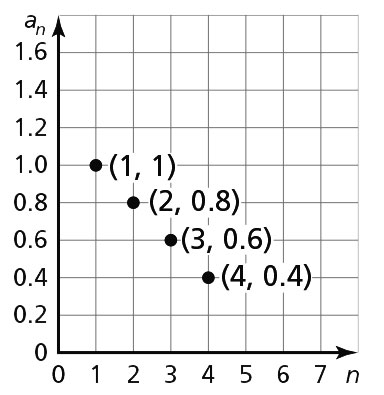
The points lie on a line. -
no; Consecutive terms do not have a common difference.
-
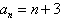 ; 28
; 28 -
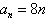 ; 200
; 200 -
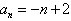 ; –23
; –23 -
a. f(n) = 2n + 5
b.
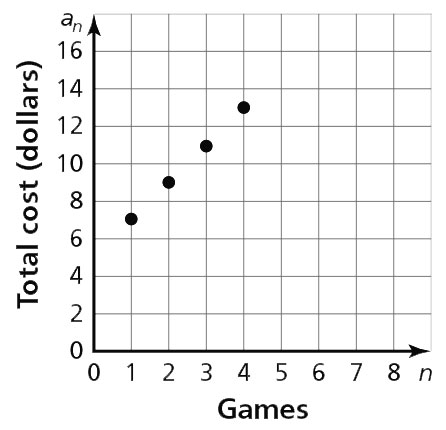
c. 12 games
Texas Tech K-12
-
Address
Texas Tech Plaza | 1901 University Ave, Lubbock, TX 79401 -
Phone
(800) 692-6877 -
Email
ttuk12@ttu.edu

