Section 5-2: Solving Systems of Linear Equations by Substitution (pages 225-230)
Section 5-2: Solving Systems of Linear Equations by Substitution (pages 225-230)
Understanding Mathematical Terms
Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.
Explorations
Read and work through the Explorations 1 and 2 and Communicate Your Answer on page 225. Then, check your answers below.
Answers to Explorations and Communicate Your Answer
Exploration 1 (page 225)
- (–2, –5); yes; Sample answer: Method 2 because both equations can be solved for y easily.
- (1, 2); yes; Sample answer: Method 1 because the first equation can be solved for x easily.
- (–1, 3); yes; Sample answer: Method 2 because the first equation can be solved for y easily.
Exploration 2 (page 225)
- Sample answer: (2, 4)
- Sample answer: y = x + 2 and 3x – 4y = –10
- Sample answer: y = x + 2 and 3x – 4y = –10; (2, 4); Because the first equation is already solved for y, substitute that expression for y in the second equation.
Communicate Your Answer (page 225)
-
Solve one of the equations for one of the variables. Substitute the expression for that variable into the other equation to find the value of the other variable. Substitute this value into one of the original equations to find the value of the remaining variable.
-
a. (–5, –1); Sample answer: The first equation can be solved for x easily.
b. (–2, 2); Sample answer: The first equation can be solved for x easily.
c. (2, –2); Sample answer: The second equation can be solved for y easily.
d. (3, 2); Sample answer: The second equation can be solved for x easily.
e. (1, –3); Sample answer: The second equation can be solved for x easily.
f. (–1, 3); Sample answer: The first equation can be solved for y easily.
Section 5-2 Lesson (pages 226-228)
In this lesson, you will learn how to solve a system using substitution. Be careful not to skip steps and watch your computations. Study and read through Examples 1 through 3. Practice with the Monitoring Progress problems as you go, and then check your answers below.
Answers to Monitoring Progress (pages 226-228)
- (–2, 8)
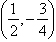
- (–1, 1)
- (–2, 0)
- (2, –2)
- (6, 17)
- (–2,
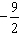 )
) - x + y = 64 and x = y + 10; 37 drama club students, 27 yearbook club students
Texas Tech K-12
-
Address
Texas Tech Plaza | 1901 University Ave, Lubbock, TX 79401 -
Phone
(800) 692-6877 -
Email
ttuk12@ttu.edu

