Understanding Mathematical Terms

Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.

Explorations

Read and work through the Explorations 1 and 2 and Communicate Your Answer on page 237. Then, check your answers below. Can a system have no solution or infinitely many solutions? You will find out in this section.

Answers to Explorations and Communicate Your Answer

Exploration 1 (page 237)

1. C = 450 + 20x; R = 20x
   

   x (skateboards)	0	1	2	3	4
   C (dollars)	450	470	490	510	530
   R (dollars)	0	20	40	60	80

   
   

   x (skateboards)	5	6	7	8	9	10
   C (dollars)	550	570	590	610	630	650
   R (dollars)	100	120	140	160	180	200

2. never; Both cost and revenue increase at the same rate, but have different initial values.

Exploration 2 (page 237)

1. 40x + 6y = 10; 20x + 3y = 5
2. 
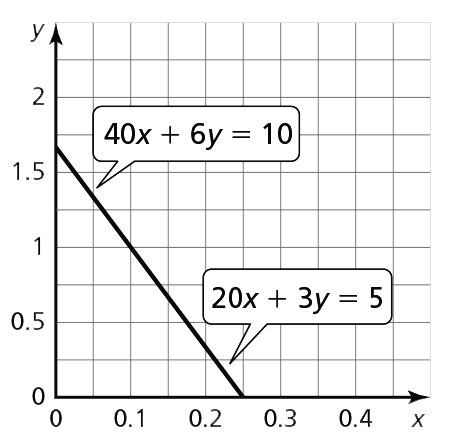
3. no; Because the equations are equivalent, there are infinitely many solutions.

Communicate Your Answer (page 237)

3. yes; Sample answer: The system y = 3x and y = 3x + 1 has no solution. The system y = 3x and 2y = 6x has infinitely many solutions.

4. a. one solution; The lines intersect at one point.
   b. no solution; The lines do not intersect.
   c. infinitely many solutions; The lines are the same line.

Section 5-4 Lesson (pages 238-240)

This lesson presents two special systems of linear equations. If the lines are parallel, then there is no solution. If the lines coincide, then there are infinitely many solutions—namely, all of the points on the line. Study and read through Examples 1 through 4. Practice with the Monitoring Progress problems as you go, and then check your answers below.

Answers to Monitoring Progress (pages 239-240)

1. infinitely many solutions
2. no solution
3. Hall A and Hall B each cost $200 for one hour of use.
4. The system has no solution; The lines still have the same slope, but they now have different y-intercepts, so they are parallel.