Understanding Mathematical Terms

Carefully read pages 3-10 in the textbook to become familiar with the terms and ideas you will be using. In your notebook, write down each bolded or highlighted core vocabulary term with its definitions and examples. It will be important to remember these terms.

Also remember to record any additional bolded vocabulary words that you find as you read through the Section Summaries.

Example definitions:

• Conjecture is an unproven statement about a general mathematical concept.
• Rule or Theorem is after a statement is proven.

Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.

Explorations

Read and work through the Explorations 1, 2, and 3, and Communicate Your Answer on page 3. Exploration 1 asks you to measure the angles of each of the quadrilaterals. Exploration 2 is about making a conjecture. You will be able to prove this conjecture true after you perform Exploration 3. Then, check your answers below.

Answers to Explorations and Communicate Your Answer

Exploration 1 (page 3)

1. 110; 90; 92; 68; 360°
2. 65; 147; 58; 90; 360°
3. 91; 79; 75; 115; 360°
   Answers will vary.

Exploration 2 (page 3)

The measures of the four angles of a quadrilateral add up to 360°.

Sample answer:

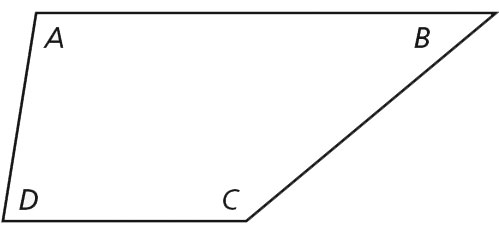
100 + 40 + 140 + 80 = 360

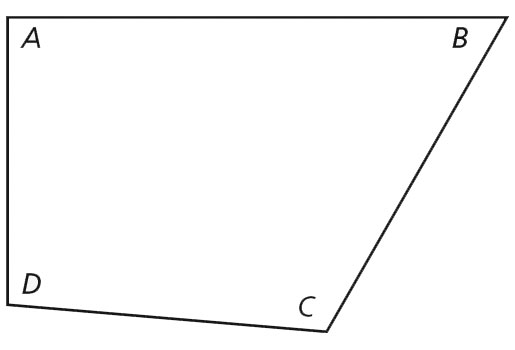
90 + 60 + 115 + 95 = 360

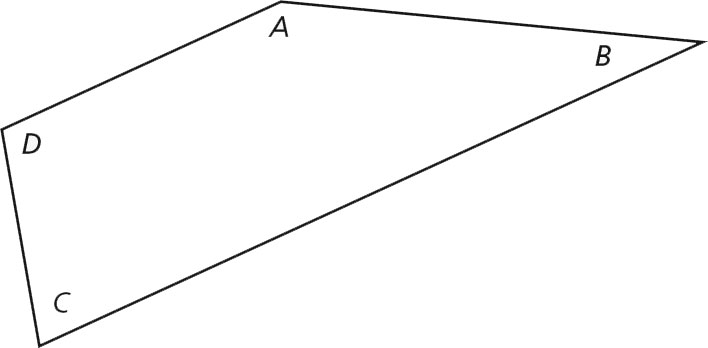
150 + 30 + 75 + 105 = 360

Divide the quadrilateral into two triangles.

The sum of the angle measures of a triangle is 180°, so the sum of the angle measures of a quadrilateral is 2(180°) = 360°.

Exploration 3 (page 3)

1. 85 + 100 + x + 80 = 360; x = 95
2. x + 78 + 60 + 72 = 360; x = 150
3. 90 + 30 + 90 + x = 360; x = 150

Communicate Your Answer (page 3)

3. Simple equations can relate parts of geometric shapes and can be used to find missing parts.
4. The corners can be arranged so the angles complete a full circle, which is 360°.

Section 1-1 Lesson (pages 4-7)

Copy down and define all core vocabulary: equation, linear equation in one variable, solution, inverse operations, and equivalent equations.

Also copy down the core concepts on pages 4, 5, 6, and 7. Remember that you can do anything you want to an equation as long as you do it to both sides. When solving equations, remember what the “equal" sign means. Picture a balance scale that is equal on both sides. To keep it balanced, you cannot remove from one side without also removing from the other side. That is what you’re doing when you solve an equation. Look at the scale below. To keep it balanced, you must do the same thing to both sides.

x + 2 = 4 

To solve, first read the equation: "a number x added to 2 is equal to 4."

x + 2 = 4	Check: substitute 2 in for x
x + 2 - 2 = 4 - 2	2 + 2 = 4
x = 2	4 = 4

Read through Examples 1, 2, 3, and 4 on pages 4-7. Be sure to look at the Four-Step Problem Solving Plan and the strategies listed on those pages. You should be familiar with these steps and strategies.  Practice with the Monitoring Progress problems as you go, and then check your answers below.

Answers to Monitoring Progress (pages 4-7)

1. n = –10; Subtract 3 from each side.
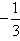2. g = ; Add to each side.
3. p = –10.4; Subtract 3.9 from each side.
4. y = –18; Multiply each side by 3.
5. x = 9; Divide each side by π.
6. w = 28; Divide each side by 0.05.
7. 38.65 sec
8. 26 = 68 – c; $42