Understanding Mathematical Terms

Refer to the English-Spanish Glossary, which starts on textbook page A39, if you need help with a definition or finding a textbook page with an example for a vocabulary word.

Explorations

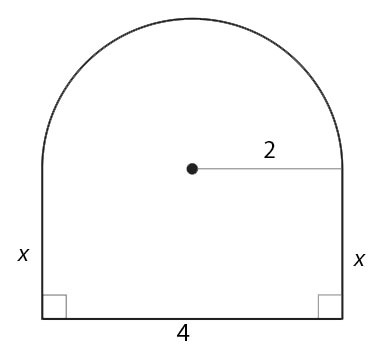
Read and work through Explorations 1 and 2 and Communicate Your Answer on page 21. Let’s look at Exploration 2, problem c.

Perimeter = circumference of half of the circle with radius 2 + the sum of the 3 sides of the rectangle.

Formulas needed are

, P = x + (2 + 2) + x, and A = lw. 

Here are some steps you may want to remember:

Step 1: Simplify and combine all like terms on both sides of the equation.

Step 2: If variables are on both sides of the equation, use the addition or subtraction property of equality to write an equivalent equation that has all of the variables on one side. It doesn’t really matter which side, but be careful with signs!

Step 3: Combine like variable terms to form one variable term.

Step 4: Write an equivalent equation that eliminates numbers that were added to or subtracted from the variable term.

Step 5: Isolate the variable by either multiplying or dividing the coefficient term or use the multiplicative inverse property.

Step 6: Check your answer using substitution or your graphing calculator.

c.

2

+ 2x + 4 = 2 + 4x

2

-2 + 2x - 2x +4 = 2 - 2

= 4x - 2x

4 = 2x

2 + x

Answers to Explorations and Communicate Your Answer

Exploration 1 (page 21)

2x + 14 = 3x + 10; x = 4; Add the side lengths of each figure to get the perimeters and set them equal to each other; P = 22

Exploration 2 (page 21)

1. x + 18 = 4x +; ; x = 4; Add the side lengths to get the perimeter. Add the area of the triangle to the area of the rectangle to get the total area. Then set the perimeter equal to the area; P = 22 ft, A = 22
2. 2x + 14 = 6x – 2; x = 4; Add the side lengths to get the perimeter. Subtract the area of the small rectangle from the area of the large rectangle to get the total area. Then set the perimeter equal to the area; P = 22 ft, A = 22
3. 2 + 2x + 4 = 2 + 4x; x = 2; Add the circumference of the semicircle to the remaining 3 side lengths to find the perimeter. Add the area of the semicircle to the area of the rectangle to find the total area. Then set the perimeter equal to the area; P = 2 + 8 ft, A = 2 + 8

Communicate Your Answer (page 21)

3. Collect the variable terms on one side of the equation and the constant terms on the other side of the equation, then solve.
4. Sample answer: 5x – 7 = 2x + 5, x = 4; –x + 3 = 4x + 13, x = –2; 7x = 6x + 4, x = 4

Section 1-3 Lesson (pages 22-24)

Copy down and define all core vocabulary and core concepts for this section. You are learning how to solve a multi-step linear equation with variables on both sides. Then you will learn about special solutions of linear equations. It is important for you to write down all steps. Do not skip steps. Remember also, if you get stuck, you can go to Big Ideas Math (see "Textbooks and Materials" in the Course Introduction). You will have access to the odd numbered problems and the online tutor.

Examples 1 and 2 are worked out for you step by step. Sometimes an equation will have no solution or an infinite number of solutions. Examples 3 and 4 demonstrate such instances.

Look at #4 and #5 on page 23.

#4.

#5.

6m –m =

(6m – 10)

5m = 5m -

5m - 5m = 5m -

-5m

0 ≠

0 ≠

no solution

Example 4 models the mathematics.

Practice with the Monitoring Progress problems as you go, and then check your answers below.

Answers to Monitoring Progress (pages 22-24)

1. x = –2
2. h =
3. n = 0
4. infinitely many solutions
5. no solution
6. k =
7. infinitely many solutions
8. 17.5 mi